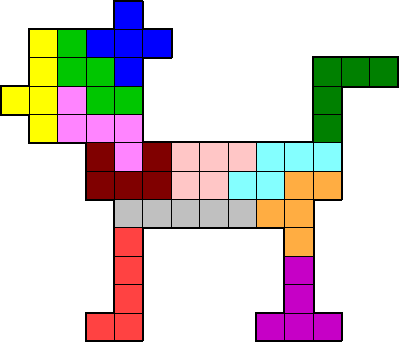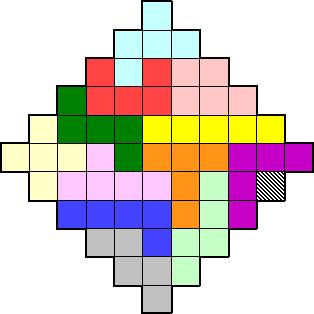LES PENTOMINOS
C'est en 1953 que le mathematicien Solomon W. Golomb présenta les polyminos : formes obtenues en juxtaposant par leurs cotés plusieurs carrés de surface identique. Avec deux carrés, on obtient un domino : Avec trois carrés, on obtient deux triminos :
Avec quatre carrés, on realise les cinq tetrominos :
Enfin, avec 5 carres, on obtient les douze pentominos que voici :
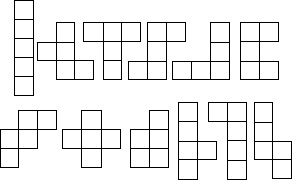
Lors de cette recherche ont été exclues les figures obtenues par symétrie ou rotation d'une figure existante. On pourrait rechercher les 35 hexominos, 107 heptominos etc... sachant qu'il n'existe aucune formule permettant de calculer le nombre de ployminos réalisés avec n carrés. Au dela de la dimension 5, il faut avoir recours à la puissance de calcul des ordinateurs. Ainsi ont été recensés 3 002 520 pentédécominos, obtenus en juxtaposant quinze carrés. Les casse-têtes utilisant les 12 pentominos sont les plus intéressants... et les seuls abordables. Ce sont aussi les plus anciens. On raconte en effet qu'un ancien maître de go les auraient découverts il y a fort longtemps.
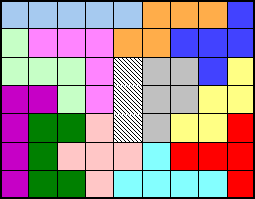
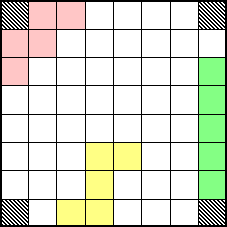
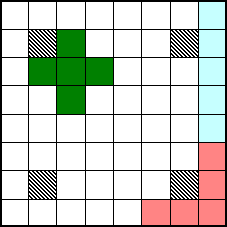
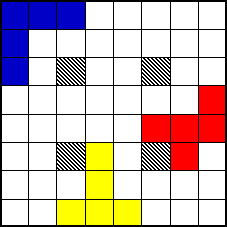
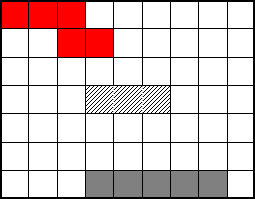
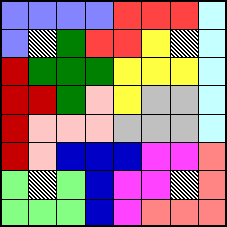
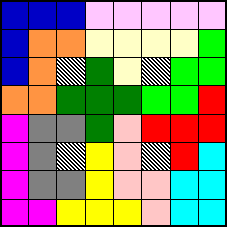
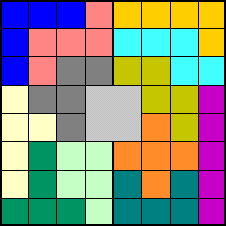
PROBLEMES FONDAMENTAUX Douze pentominos, cela fait 60 cases. En supposant une boîte rectangulaire dans laquelle il faudrait faire rentrer les douze pentominos, plusieurs possibilités apparaîssent : une boîte 6X10 2339 solutions différentes une boîte 5X12 1010 solutions différentes une boîte 4X15 368 solutions différentes une boîte 3X20 2 solutions seulement En voici quelques-unes. Saurez-vous les compléter ? 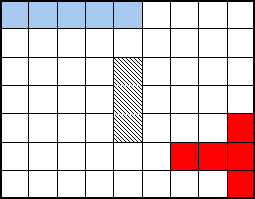6 X 10  SOLUTION 5 X 12  SOLUTION 4 X 15  SOLUTION 3 X 20  SOLUTION
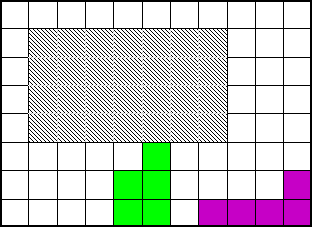
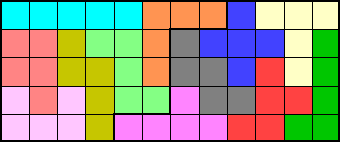
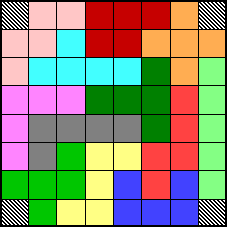
L'ECHIQUIER Comment remplir un échiquier de 64 cases avec les 12 pentominos ? Et bien en enlevant 4 cases, tout simplement !
SOLUTION	SOLUTION
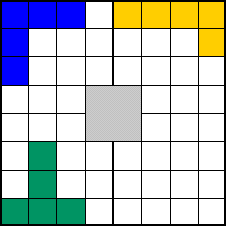
SOLUTION	SOLUTION
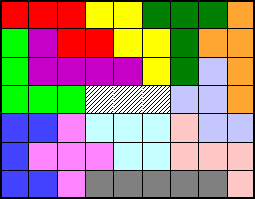
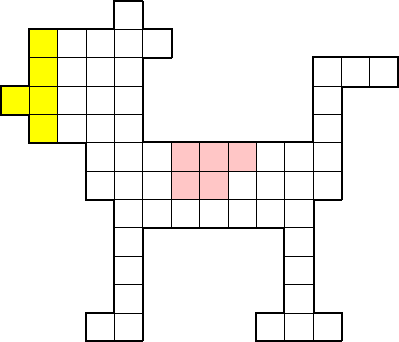
LES FERMES Voici quelques fermes avec leurs cours
SOLUTION
SOLUTION	SOLUTION
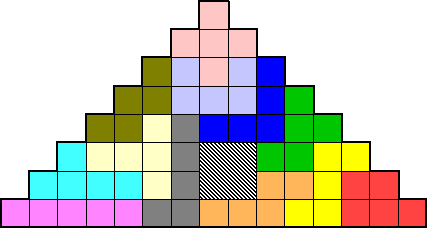
FORMES VARIEES
LE PENTOMINET SOLUTION
LA PYRAMIDE SOLUTION
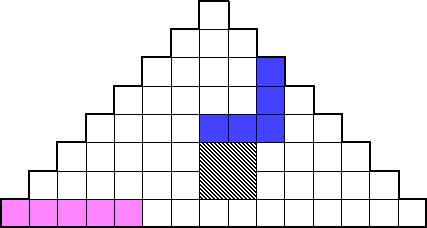
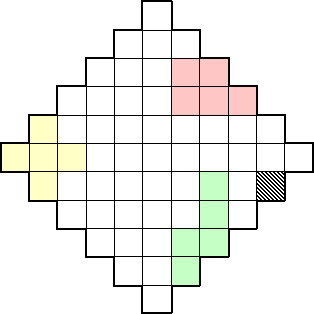
LE LOSANGE SOLUTION
LA 3ème DIMENSION Quelques pistes...
SOLUTIONS 6 X 10   5 X 12   4 X 15   3 X 20   ECHIQUIERS 8 X 8